Functions related to random number generators for various distributions. More...

Functions
double	powerlaw_rand (std::vector< double > &param, std::mt19937 &_engine)
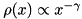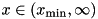	Generates a random real number following a power-law distribution of the form $\rho(x) \propto x^{-\gamma}$ with $x\in(x_\mathrm{min},\infty)$ . More...

double	powerlaw_m1 (std::vector< double > &param)
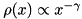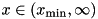	Returns the first moment of a power-law distribution of the form $\rho(x) \propto x^{-\gamma}$ with $x\in(x_\mathrm{min},\infty)$ . More...

double	powerlaw_hardcutoff_rand (std::vector< double > &param, std::mt19937 &_engine)
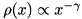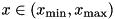	Generates a random real number following a power-law distribution of the form $\rho(x)\propto x^{-\gamma}$ with $x\in(x_\mathrm{min},x_\mathrm{max})$ (i.e., hard cut-off). More...

double	powerlaw_hardcutoff_m1 (std::vector< double > &param)
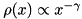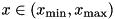	Returns the first moment of a power-law distribution of the form $\rho(x) \propto x^{-\gamma}$ with $x\in(x_\mathrm{min},x_\mathrm{max})$ (i.e., hard cut-off). More...

double	exponential_rand (std::vector< double > &param, std::mt19937 &_engine)
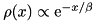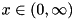	Generates a random real number following an exponential distribution of the form $\rho(x)\propto \mathrm{e}^{-x/\beta}$ with $x\in(0,\infty)$ . More...

double	exponential_m1 (double param)
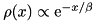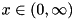	Returns the first moment of an exponential distribution of the form $\rho(x)\propto \mathrm{e}^{-x/\beta}$ with $x\in(0,\infty)$ . More...

double	gamma_rand (std::vector< double > &param, std::mt19937 &_engine)
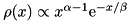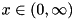	Generates a random real number following a gamma distribution of the form $\rho(x)\propto x^{\alpha-1}\mathrm{e}^{-x/\beta}$ with $x\in(0,\infty)$ . More...

double	gamma_m1 (std::vector< double > param)
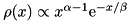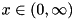	Returns the first moment of a gamma distribution of the form $\rho(x)\propto x^{\alpha-1}\mathrm{e}^{-x/\beta}$ with $x\in(0,\infty)$ . More...

Detailed Description

Functions related to random number generators for various distributions.